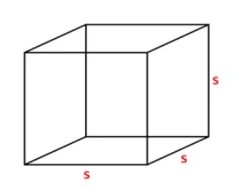
Kubus adalah bangun ruang tiga dimensi yang dibatasi oleh enam bidang sisi yang berbentuk bujur sangkar. Kubus memiliki 6 sisi, 12 rusuk dan 8 titik sudut. Kubus juga disebut bidang enam beraturan, selain itu juga merupakan bentuk khusus dalam prisma segiempat.

Gambar diatas dinamakan kubus ABCD.EFGH. Dari gambar di atas tampak bahwa kubus memiliki unsur-unsur sebagai berikut :
- Sisi/bidang kubus merupakan datar yang membatasi kubus. Kubus memiliki 6 buah sisi yang semuanya berbentuk persegi, yaitu sisi bawah = ABCD, sisi atas = EFGH, sisi depan (ABFE), sisi belakang = CDHG, sisi kanan = ADHE, dan sisi kiri = BCGF.
- Rusuk merupakan garis potong antara dua sisi bidang kubus. Kubus memiliki 12 buah rusuk, yaitu AB, BC, CD, DA, EF, FG, GH, HE, AE, BF, CG, dan DH.
- Titik sudut merupakan titik potong antara tiga rusuk. Kubus ABCD. EFGH memiliki 8 buah titik sudut, yaitu titik A, B, C, D, E, F, G, dan H.
- Diagonal bidang merupakan garis yang menghubungkan dua titik sudut yang saling berhadapan dalam satu sisi/bidang. Pada kubus ABCD.EFGH terdapat 8 buah titik sudut yaitu : A, B, C, D, E, F, G, H, .
- Diagonal ruang merupakan HB yang menghubungkan dua titik sudut yang saling berhadapan dalam satu ruang. Terdapat empat diagonal ruang yang sama panjangnya dan saling berpotongan di tengah-tenagh yaitu AG = BH = CE = DF.
- Bidang diagonal merupakan bidang yang dibentuk oleh dua diagonal bidang dan dua rusuk yang saling sejajar. Terdapat 6 buah bidang diagonal yaitu : ACGE, BDHF, ABGH, CDEF, ADGF, dan BCHE.
Sifat-sifat Kubus
Kubus memiliki sifat-sifat sebagai berikut:
- Semua sisi merupakan persegi
- Semua rusuk sama panjang
- Semua diagonal bidang sama panjang
- Semua diagonal ruang sama panjang
- Semua bidang diagonal berbentuk persegi panjang.
Jaring-jaring Kubus
Jaring-jaring kubus dibentuk dari 6 buah persegi yang apabila dirangkaikan akan membentuk suatu kubus. Ada beberapa macam bentuk jaring-jaring kubus, diantaranya tampak seperti gambar berikut.

Rumus-rumus Kubus
1. Volume kubus
Pada dasarnya untuk mencari volume suatu bidang ruang digunakan rumus
Volume = Luas alas x tinggi
Dimana luas alas kubus adalah persegi dan panjang sisi alasnya sama dengan tinggi kubus
Sehingga:
volume kubus = panjang rusuk × panjang rusuk × panjang rusuk
= s × s × s
= s3
Jadi, volume kubus dapat dinyatakan sebagai berikut.
V = s3
2. Luas Permukaan
Untuk mencari luas permukaan kubus, kita akan menghitung luas jaring-jaring kubus yang berjumlah 6 buah persegi yang sama besar dan kongruen.
Sehingga :
Luas permukaan kubus = luas jaring-jaring kubus
= 6 × (s × s)
= 6 × s2
= 6 s2
Jadi, luas permukaan kubus dapat dinyatakan dengan rumus sebagai berikut.
L = 6s2
Contoh soal
1. ABCD.EFGH adalah kubus dengan panjang rusuk 5 cm. Hitunglah volume dan luas permukaan bangun tersebut!
Penyelesaian:
= 150 cm2
2. Hitunglah panjang rusuk suatu kubus jika diketahui memiliki jaring-jaring kubus dengan luas 294 cm2!
Penyelesaian:
Luas permukaan kubus = 6s2
Diperoleh 294 = 6 · s2
s2 = 294
6
s2 = 49
s = 7
Jadi, panjang rusuk kubus tersebut adalah 7 cm.
 Teknobae.com Berita Teknologi, Review Gadget, Laptop, Komputer, Smartphone, Handphone
Teknobae.com Berita Teknologi, Review Gadget, Laptop, Komputer, Smartphone, Handphone