Memahami Peluang, Ruang Sampel, Frekuensi Harapan Dan Komplemen Kejadian (Pembahasan Lengkap)

admin 19/07/2022 Matematika 18 Views

Pembahasan matematika kali ini, akan kita bahas konsep-konsep yang berhubungan dengan peluang. Berbicara mengenai peluang, tentu kita sudah tahu apa itu peluang. Misalnya seperti saat kita mengatakan “berapa persen peluang saya lulus ujian”, “bagaimana peluang saya diterima di kampus tersebut?”.

Nah sekarang, dalam matematika kita juga akan mempelajari teori peluang atau terkadang disebut juga dengan probabilitas.

Apa itu Peluang?

Peluang adalah suatu nilai untuk mengukur tingkat kemungkinan terjadinya suatu kejadian yang tidak pasti (uncertainty event).

Masih bingung dengan definisi atas ?

Anda pernah bermain ular tangga atau ludo ?. Ketika kita berjalan berapa langkah, kita harus melempar dadu terlebih dahulu.

Seperti yang kita ketahui, angka pada dadu terdiri angka 1 , 2, 3, 4, 5 dan 6. Kadang-kadang muncul angka 1, kadang-kadang muncul 3. Bahkan bisa saja muncul angka yang sama setelah dua kali kita melempar dadu.

Kemungkinan angka-angka yang muncul tersebutlah yang kita sebut sebagai salah satu contoh dari peluang.

Beberapa istilah dalam Peluang yang perlu diketahui

Ada beberapa istilah yang perlu kita ketahui, dimana istilah tersebut sering digunakan dalam konsep peluang. Istilah-istilah tersebut adalah :

Ruang Sampel
Himpunan semua kejadian atau hasil yang mungkin dari suatu percobaan.

Titik Sampel
Titik Sampel adalah anggota dari ruang sampel

Kejadian
Kejadian adalah himpunan bagian dari ruang sampel.

n(S)
n(S) adalah notasi untuk menyatakan banyaknya anggota sampel

Contoh 1 :

Bila kita melempar sebuah dadu, maka akan didapatkan :

Titik Sampelnya adalah angka – angka : (1) , (2), (3), (4), (5), (6)
Ruang sampel (S) = {1, 2, 3, 4, 5, 6}
n(S) = 6

Contoh 2:

Bila kita melempar dadu, maka akan diperoleh :

Titik Sampelnya adalah : (Gambar) , (Angka)
Ruang sampel (S) = {Gambar, Angka}
n(S) = 2.

Bagaimana Cara Menentukan Ruang Sampel?

Dalam menentukan ruang sampel, terdapat beberapa, diantaranya adalah :

1. Dengan cara mendaftarkan satu-persatu.

Cara ini adalah cara yang sangat mudah dan sederhana, cukup disebutkan satu-persatu anggota ruang sampelnya.

Contoh :

Ketika kita melempar uang koin, maka ada dua kemungkinan yang muncul, yaitu : sisi angka (A) atau sisi gambar (G). Ruang sampelnya cukup kita sebutkan satu-persatu, sehingga ditulis :

S = {A, G}

Nah bagaimana jika kita lempar dua koin sekaligus ?

Jika koin pertama muncul angka (A) , sedangkan koin kedua muncul gambar (G), maka kejadian dari pelemparan tersebut adalah (A, G).

Semua hasil yang mungkin terjadi dari percobaan tersebut adalah (A, G), (G, A), (A, A), dan (G, G).

Dengan demikian, pelemparan dua koin akan kita dapatkan:

Ruang sampel (S) : {(A, G), (G, A), (A, A), (G, G)}.
Titik sampel : (A, G), (G, A), (A, A), dan (G, G).
Kejadian : {(A, G)}, {(G, A)}, {(A, A)}, atau {(G, G)}.
Banyaknya ruang sampel, n(S) = 4

2. Dengan cara membuat tabel

Untuk pembuatan ruang sampel dengan tabel, kita ambil contoh pelemparan dua dadu. Ruang sampelnya dapat dibuatkan tabel seperti tabel di bawah ini :

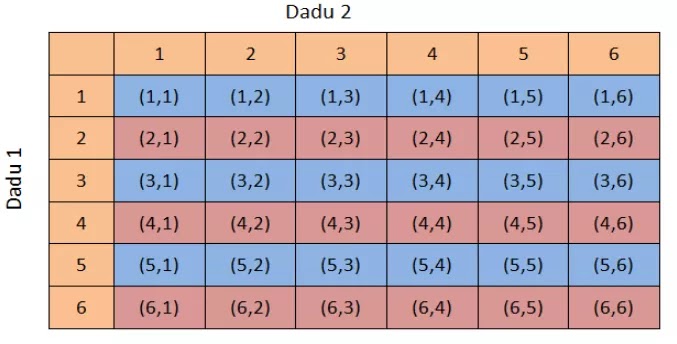
Dengan demikian, pelemparan dua dadu tersebut akan di dapatkan:

Ruang Sampel (S) : {(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(2,1),(2,2),(2,3),(2,4),(2,5),(2,6),(3,1),(3,2),(3,3),(3,4),(3,5),(3,6),(4,1),(4,2),(4,3),(4,4),(4,5), (4,6),(5,1),(5,2),(5,3),(5,4),(5,5),(5,6),(6,1),(6,2),(6,3),(6,4),(6,5),(6,6)}.
Titik Sampel (1,2) berarti Dadu ke-1 muncul angka 1 dan Dadu ke-2 muncul angka 2.
Banyaknya ruang sampel , n(S) = 36

3. Dengan cara membuat diagram pohon

Sebuah koin memiliki Angka (A) dan Gambar (G). Jika kita melempar tiga koin sekaligus, maka kita dapat membuat Ruang Sampel ketiga koin tersebut ke dalam diagram pohon seperti yang ditunjukkan oleh Gambar dibawah ini :

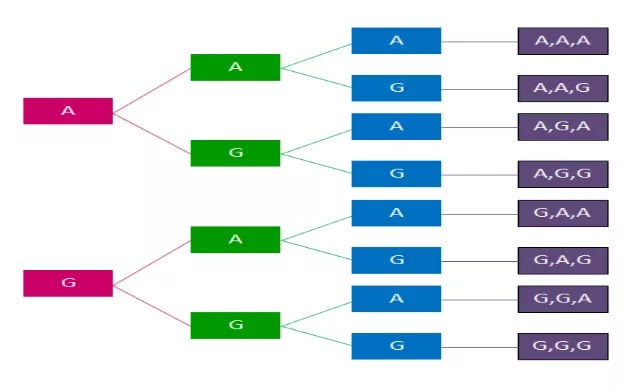
Dari percobaan pelemparan tiga koin, maka akan didapatkan :

Ruang sampel (S )= {(A, A, A), (A, A, G), (A, G, A), (A, G, G), (G, A, A), (G, A, G), (G, G, A), (G, G, G)}.
Banyaknya ruang sampel, n(S) = 8

Peluang Suatu Kejadian

Nah sekarang kita akan mencoba memahami maksud dari suatu peluang kejadian.

Peluang suatu kejadian adalah perbandingan banyaknya kejadian (titik sampel) dengan banyaknya ruang sampel.

Nah itu adalah maksud atau pengertian dari peluang suatu kejadian. Lalu bagaimana rumus untuk menghitung peluang suatu kejadian ?

Rumus untuk menghitung peluang suatu kejadian adalah :

P(A)=

n(A)n(S)

Keterangan :

P(A) adalah peluang kejadian A
n(A) adalah kejadian A
n(S) adalah banyaknya ruang sampel

Nilai peluang berada diantara 0 dan 1 atau 0 ≤ P(A) ≤ 1

Komplemen Suatu Kejadian

Sekarang kita akan mencoba memahami maksud dari kompelemen suatu kejadian.Yang dimaksud dengan komplemen suatu kejadian adalah himpunan kejadian yang mungkin terjadi selain kejadian tersebut.

Jika A adalah suatu kejadian, maka komplemen kejadian A adalah kejadian bukan A, ditulis dengan A’ (dibaca: A komplemen).

Masih bingung dengan definisi di atas ?

Contoh:

Kita ambil kasus dalam pelemparan sebuah dadu. Kompelemen dari munculnya kejadian angka 3 adalah : 1, 2, 4, 5, 6. Jadi komplemen 3 adalah angka-angka yang terdapat dalam ruang sampel dadu tersebut, namun selain 3.

Masih dalam kasus pelemparan sebuah dadu. Komplemen dari munculnya kejadian angka 2 adalah : 1, 3, 4, 5, 6. Jadi kita tinggal sebutkan selain angka 2 dengan catatan titik sampel/kejadian yang kita sebutkan merupakan bagian dari ruang sampel tersebut.

Hubungan peluang kejadian A dan kejadian bukan A ditentukan oleh rumus berikut:

P(A) + P(A’) = 1
P(A’) = 1 – P(A)
P(A) = 1 – P(A’)

Frekuensi Harapan

Frekuensi harapan adalah banyaknya kejadian yang bisa diharapkan dari beberapa kali percobaan yang dilakukan.

Misal A adalah sebuah kejadian pada ruang sampe S, jika percobaan dilakukan n kali maka frekuensi harapan kejadian A atau f(A) dari n kali percobaan adalah :

f(A) = n x P(A)

Keterangan :