Maka pada pembahasan kali ini kita akan masuk ke pembahasan soal-soal luas dan keliling segitiga beserta pembahasannya secara lengkap. Nah, Bagi anda yang ingin mempelajari konsep penting dari bangun datas segitiga, silahkan kunjungi artikel dengan judul : Jenis-jenis segitiga dan rumus luas keliling segitiga.
Soal No.1
Sebuah segitiga memiliki alas sebesar 5 cm dan tinggi 6 cm. Hitunglah luas segitiga tersebut ?
Pembahasan
Luas Segitiga =
12
x alas x tinggi
Luas Segitiga =
12
x 5 x 6
Luas Segitiga = 15 cm2
Soal No.2
Jika diketahui sebuah segitiga bangun datar yang memiliki sisi-sisi diantaranya sisi a, sisi b dan sisi c dengan masing-masing panjang sebesar 12 cm, 8 cm, dan 5 cm. Tentukan keliling segitiga tersebut ?
Pembahasan
Keliling Segitiga = a + b + c
Keliling Segitiga = 12 + 8 + 5
Keliling Segitiga = 25 cm
Soal No.3
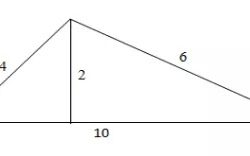
Hitunglah luas dan keliling segitiga di bawah ini :
Pembahasan
Untuk Luas Segitiga
a = 10 cm
t = 2 cm
Luas Segitiga =
12
x alas x tinggi
Luas Segitiga =
12
x 10 x 2
Luas Segitiga = 10 cm2
Untuk Keliling Segitiga
Keliling Segitiga = Sisi a + Sisi b + Sisi c
Keliling Segitiga = 10 + 6 + 4
Keliling Segitiga = 20 cm
Soal No.4
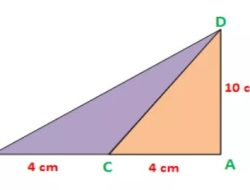
Diketahui segitiga seperti gambar dibawah yang memiliki panjang sisi BC sebesar 4cm, panjang sisi AC sebesar 4 cm dan panjang sisi AD sebesar 10 cm.
Hitunglah luas dari :
Pembahasan
Untuk Luas Δ ACD
Dari gambar di atas, tampak bahwa :
alas = panjang sisi AC = 4 cm
tinggi = panjang sisi AD = 10
Luas Δ ACD =
12
x alas x tinggi
Luas Δ ACD =
12
x AC x AD
Luas Δ ACD =
12
x 4 x 10
Luas Δ ACD = 20 cm2
Untuk Luas Δ BCD
Dari gambar di atas, tampak bahwa :
alas = panjang sisi BC = 4 cm
tinggi = AD = 10 cm (tingginya tetap AD, karena tinggi segitiga adalah garis yang tegak lurus dengan alasnya)
Luas Δ BCD =
12
x 4 x 10
Luas Δ BCD = 20 cm2
Untuk Luas Δ ABD
Dari gambar diatas tampak bahwa :
alas = panjang sisi BC + panjang sisi AC = 4 cm + 4 cm = 8 cm
tinggi = panjang sisi AD = 10 cm
Luas Δ BCD =
12
x 8 x 10
Luas Δ BCD = 40 2
Soal No.5
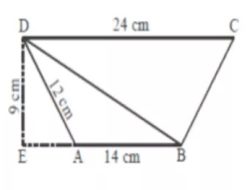
Diketahui sebuah segitiga seperti gambar di bawah ini, dimana panjang sisi DE = 9 cm, panjang sisi AD = 12 cm, panjang sisi AB = 14 cm, panjang sisi CD = 24 cm.
Hitungalah luas segitiga :
- Luas Δ ABD
- Luas Δ BCD
- Luas Δ ABCD
Pembahasan
Untuk Luas Δ ABD
alas = panjang sisi AB = 14 cm
tinggi = panjang DE = 9 cm (karena tinggi segitiga adalah garis yang tegak lurus dengan alasnya)
Luas Δ ABD =
12
x alas x tinggi
Luas Δ ABD =
12
x 14 x 9
Luas Δ ABD = 63 cm2
Untuk Luas Δ BCD
alas = panjang sisi CD = 24 cm
tinggi = panjang DE = 9 cm (karena tinggi segitiga adalah garis yang tegak lurus dengan alasnya)
Luas Δ BCD =
12
x alas x tinggi
Luas Δ BCD =
12
x 24 x 9
Luas Δ BCD = 108 cm2
Untuk Luas Δ ABCD
Luas Δ ABCD = Luas ΔABD + Luas ΔBCD
Luas Δ ABCD = 63 cm2 + 108 cm2
Luas Δ ABCD = 171 cm2
Soal No.6
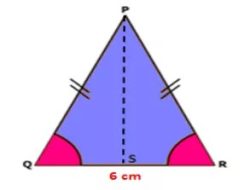
Diketahui keliling segitiga sama kaki PQR adalah 16 cm. Jika panjang sisi QR 6 cm, berapakah luasnya ?
Pembahasan
Keliling Δ PQR = QR + PQ + PR
Keliling Δ PQR = QR + 2PQ (Karena sama kaki, maka PQ = PR)
16 = 6 + 2PQ
2PQ = 16 – 6
2PQ = 10
PQ =
102
= 5 cm
Jadi panjang sisi PQ dan QR masing-masing bernilai 5 cm
Untuk mencari luas, harus diketahui tinggi terlebih dahulu. Pada gambar di atas, tingginya adalah sisi PS.
RS = 1/2 dari QR = 3 cm
PR2 = RS2 + PS2
52 = 32 + PS2
25 = 9 + PS2
PS2 = 25 – 9
PS2 = 16
PS = √16 = 4 cm
Jadi tingginya adalah 4 cm
Luas Δ PQR =
12
x alas x tinggi
Luas Δ PQR =
12
x 6 x 4
Luas Δ PQR = 12 cm2
Soal No.7
Sebuah Segitiga siku-siku Δ ABC diketahui luasnya sebesar 24 cm² dan tinggi 8 cm . Hitunglah keliling Δ ABC tersebut ?
Pembahasan
Luas Δ ABC =
12
x a x t
24 =
12
x a x 8
24 = 4a
a =
244
= 6 cm
Untuk mencari keliling kita harus mengetahui panjang ke tiga sisi dari segitiga ABC diatas.Dalam gambar segitiga di atas, alas = sisi AB. Jadi panjang sisi AB adalah 6 cm. Yang belum diketahui adalah sisi BC. Kita dapat mencari sisi BC dengan menggunakan rumus phytagoras.
BC2 = AB2 + AC2
BC2 = 62 + 82
BC2 = 36 + 64
BC2 = 100
BC = √100 = 10 cm
Keliling Δ ABC = AB + AC + BC
Keliling Δ ABC = 6 + 8 + 10
Keliling Δ ABC = 24 cm
Soal No.8
Pak Budi berencana membuat stempel yang berbentuk segitiga sama kaki sebanyak 8 buah. Stempel segitiga tersebut memiliki alas 8 cm dan tinggi 5 cm. Tiap Tiap 1 cm2 membutuhkan biaya Rp 200. Berapa biaya yang dibutuhkan untuk membuat 8 buah stempel tersebut ?
Pembahasan
Luas Segitiga =
12
x a x t
Luas Segitiga =
12
x 8 x 5
Luas Segitiga = 20 cm2
Jadi 1 buah stempel = 20 cm2
Karena 1 cm2 biayanya Rp 200,- maka :
Harga 1 stempel = 200 x 20 = Rp 4000
Harga 8 stempel = 8 x 4000 = Rp 32000
Soal No.9
Reza gemar berolahraga. Pada suatu hari Reza berlari mengelilingi lapangan yang berbentuk segitiga dengan panjang sisi-sisinya 20 m, 30 m, dan 40 m. Pada saat itu Reza hanya mampu berlari sebanyak 3 kali putaran. Berapakah panjang lintasan lari yang dilakukan Reza ?
Pembahasan
Keliling = panjang semua sisi
Keliling = 20 + 30 + 40
Keliling = 90 m
Reza berlari sebanyak 3 x putaran, sehingga :
Panjang lintasan = 90 x 3 = 270 m
Jadi, panjang lintasan larinya adalah 270 meter.
Soal No.10
Sebuah segitiga sama kaki mempunyai keliling 39 cm. Apabila panjang sisi alasnya 15 maka panjang sisi yang sama adalah…?
Pembahasan
Keliling = 39 cm
Sisi a = Sisi alas = 15 cm
Keliling Segitiga = Sisi a + Sisi b + Sisi c
Ingat..segitiga sama kaki adalah segitiga yang memiliki dua sisi yang sama panjang dimana sisi sama panjangnya ini kita namakan sebagai kakinya.
Jadi kita anggap Sisi b dan Sisi c adalah sisi yang sama panjang yang kita anggap sebagai Sisi K, sedangkan Sisi a sebagai alas. Dengan demikian kita dapat tulis kembali rumus keliling segigita sama kaki menjadi :
Keliling Segitiga = Sisi a + (2 x Sisi K)
39 = 15 + (2 x Sisi K)
39 – 15 = 2Sisi K
24 = 2Sisi K
Sisi K = 12 cm
Jadi, panjang sisi-sisi yang sama adalah 12 cm.
Soal No.11
Jika alas dari segitiga 9 cm dan tinggi 8 cm maka luas dari segitiga tersebut adalah ….?
Pembahasan
alas (a) = 9 cm
tinggi (t) = 8 cm
Luas Segitiga =
12
x alas x tinggi
Luas Segitiga =
12
x 9 x 8
Luas Segitiga = 36 cm2
Soal No.12
Sebuah segitiga sama kaki memiliki keliling 65 cm. Jika panjang alas 17cm maka panjang sisi yang lain adalah …?
Pembahasan
Keliling = 65 cm
Sisi a = Sisi alas = 17 cm
Keliling Segitiga = Sisi a + Sisi b + Sisi c
Karena segitiga sama kaki memiliki dua sisi yang sama panjang, maka kita anggap Sisi b dan Sisi c adalah sisi yang sama panjang yang kita anggap sebagai Sisi K, sedangkan Sisi a sebagai alas. Dengan demikian kita dapat tulis kembali rumus keliling segigita sama kaki menjadi :
Keliling Segitiga = Sisi a + (2 x Sisi K)
65 = 17 + (2 x Sisi K)
65 – 17 = 2Sisi K
58 = 2Sisi K
Sisi K = 29 cm
Jadi, panjang sisi-sisi yang lain adalah 29 cm.
Soal No.13
Segitiga sama sisi memiliki panjang sisi 60 cm dan tinggi 52 cm. Hitunglah keliling dan luas nya ?
Pembahasan
Panjang ketiga sisi pada segitiga sama sisi adalah sama panjangnya. Maka :
Sisi a = Sisi b = Sisi c = 60 cm
tinggi = 52 cm
Keliling Segitiga = Sisi a + Sisi b + Sisi c
Keliling Segitiga = 60 a + 60 + 60
Keliling Segitiga = 180 cm
Luas Segitiga =
12
x alas x tinggi
Luas Segitiga =
12
x 60 x 52
Luas Segitiga = 1560 cm2
Soal No.14
Sebuah segitiga tumpul yg memiliki panjang alasnya 10 cm dan juga memiliki tinggi 4 cm. Cari dan Hitung lah luas segitiga tersebut ?
Pembahasan
alas (a) = 10 cm
tinggi (t) = 4 cm
Luas Segitiga Tumpul =
12
x alas x tinggi
Luas Segitiga Tumpul =
12
x 10 x 4
Luas Segitiga Tumpul = 20 cm2
Jadi, luas segitiga tumpul tersebut adalah 20 cm2


 Teknobae.com Berita Teknologi, Review Gadget, Laptop, Komputer, Smartphone, Handphone
Teknobae.com Berita Teknologi, Review Gadget, Laptop, Komputer, Smartphone, Handphone