Contoh Soal Persamaan Kuadrat dan Pembahasannya

admin 20/07/2022 Matematika 16 Views

Pembahasan pada artikel kali ini yaitu tentang persamaan kuadrat. Topik materi ini adalah materi yang paling sering digunakan dalma memecahkan suatu persoalan dan juga soal yang paling sering diujikan.

Nah, beranjak dari sering munculnya soal-soal tentang persamaan kuadrat, maka memahami variasi soalnya merupakan suatu upaya yang bagus bagi kita ketika nanti menghadapi ujian yang berkaitan dengan materi persamaan kuadrat.

Mencari Akar-Akar Persamaan Kuadrat

Bentuk umum dari persamaan kuadrat adalah :

ax2 + bx + c = 0 ,a≠0

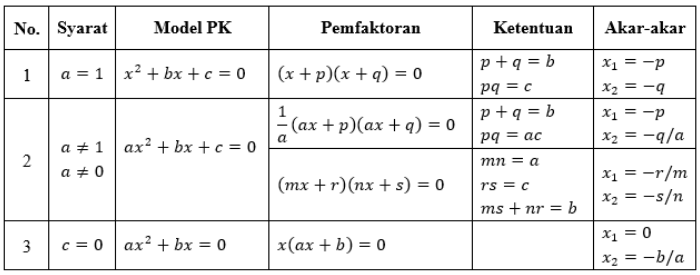
Dari persamaan kuadrat tersebut terdapat tiga cara dalam mencari akar-akar dari persamaan kuadrat tersebut,yaitu :

  • Dengan cara mengfaktorkan
  • Dengan cara melengkapkan bentuk kuadrat
  • Dengan menggunakan rumus ABC

Jumlah, Selisih dan Hasil Kali Akar-Akar

Kita dapat mencari penjumlahan, selisih ataupun perkalian akar-akar dari persamaan ax2 + bx + c = 0 tanpa mengetahui nilai dari akar-akarnya terlebih dahulu. Berikut ini adalah rumus dalam mencari jumlah, selisih dan hasil kali akar-akar :

1. Jumlah Akar : x1 + x2 = 

-ba

2. Perkalian Akar : x1 . x2 =

ca

3. Selisih Akar : |x1-x2| =

√D|a|

 

Bagi anda yang berkeinginan mereview teori-teori lainteori tentang “Persamaan Kuadrat“, dapat mengunjungi artikel yang berjudul : Rumus Diskrimina, Sifat-Sifat dan Bentuk Simetris Akar Persamaan Kuadrat.

Contoh Soal Persamaan Kuadrat dan Pembahasannya

Soal No.1

Jika sebuah persamaan kuadrat x2 – 3x + 2. Maka nilai a, b dan c adalah :

A. 1, -3, 2
B. 1, 3, 2
C. 1, -3, -2
D. 1, 3, -2

Pembahasan

Seperti yang kita ketahui, Bentuk umum persamaan kuadrat yaitu y = ax2 + bx + c dengan a ≠ 0 dan a merupakan koefisien dari x2, b merupakan koefisien dari x, sedangkan c adalah koefisien konstanta atau biasa disebut juga suku bebas.

Dari persamaan : x2 – 3x + 2, maka dapat kita simpulkan bahwa : a = 1, b = -3 dan c = 2

Jawab : A

Soal No.2

Jika sebuah persamaan kuadrat x2 – 6. Maka nilai a, b dan c adalah :

A. 1, -6, 1
B. 1, -6, 0
C. 1, 0, -6
D. 1, 0, 6

Pembahasan

Ingat, persamaan kuadrat secara umum : y = ax2 + bx + c membolehkan b dan c diset 0, namun tidak berlaku untuk a. Sehingga terkadang kita akan mendapat persamaan kuadrat seperti : y = ax2 + bx atau y = ax2 + c

Dengan demikian, dari persamaan kuadrat : x2 – 6, maka nilai a=1, b = 0 dan c = -6.

Jawab: C

Soal No.3

Jika Bentuk umum dari persamaan x2 - 16 = 7(x - 4) adalah ax2 + bx + c = 0, maka nilai a, b, c secara berturut-turut adalah :

A. 1, -7 dan 12
B. 1, 7 dan 12
C. 1, -16 dan 7
D. 1, 7 dan 20

Pembahasan

Terlebih dahulu ubahlah persamaan x2 - 16 = 7(x - 4) kedalam bentuk ax2 + bx + c = 0

⇔ x2 – 16 = 7(x – 4)
⇔ x2 – 16 = 7x – 28
⇔ x2 – 16 – 7x + 28
⇔ x2 – 7x + 12

Dengan demikian nilai a = 1, b = -7 dan c = 12

Jawab : A

Soal No.4

Jika Bentuk umum dari persamaan (2x - 1)(x - 5) adalah ax2 + bx + c = 0, maka nilai a, b, c secara berturut-turut adalah :

A. 2, 10 dan 6
B. 2, -11 dan 6
C. 2, 11 dan 7
D. 2, -11 dan -6

Pembahasan

Terlebih dahulu ubahlah persamaan (2x - 1)(x - 5) kedalam bentuk ax2 + bx + c = 0

⇔ (2x – 1)(x – 5)
⇔ 2x2 – 10x – x + 6
⇔ 2x2 – 10x – x + 6
⇔ 2x2 – 11x + 6

Dengan demikian : nilai a = 2, b = -11 dan c = 6

Jawab : B

Soal No.5

Jika Bentuk umum dari persamaan :

2(x-1)

 + 

1(x-2)

 = 2 adalah ax2 + bx + c = 0, maka nilai a, b, c secara berturut-turut adalah :

A. 2, -9 dan 9
B. 2, 9 dan 9
C. 2, 11 dan 9
D. 2, -11 dan 9

Pembahasan

Kedua ruas kita kalikan dengan (x – 1)(x – 2), dengan (x – 1)(x – 2) ≠ 0
⇔ 2(x – 2) + (x – 1) = 2(x – 1)(x – 2)
⇔ 2x – 4 + x – 1 = 2(x2 – 3x + 2)
⇔ 3x – 5 = 2x2 – 6x + 4
⇔ 2x2 – 9x + 9 = 0

Dengan demikian : nilai a = 2, b = –9 dan c = 9

Jawab : A

Soal No.6

Himpunan penyelesaian dari persamaan x2 + 5x + 6 adalah :

A. {-2, 3}
B. {-2, -3}
C. {2, 3}
D. {3, -2}

Pembahasan

Dalam hal ini Himpunan penyelesaian adalah akar-akar dari persamaan kuadrat tersebut. Dalam mencari himpunan penyelesaiannya terdapat tiga cara, yaitu :

  • Dengan mengfaktorkan
  • Dengan Melengkapi Kuadrat
  • Dengan menggunakan rumus ABC

Untuk mempelajari secara lebih detil yang disertai juga dengan contoh latihan dari ketiga metode tersebut, silahkan kunjungi artikel yang berjudul : Tiga Metode Penyelesaian Persamaan Kuadrat.

Untuk soal diatas, kita menggunakan mengfaktorkan , yaitu :
⇔ x2 + 5x + 6 = 0
⇔ (x + 2)(x + 3) = 0
⇔ x1 = -2 atau x2 = -3

Jadi himpunan penyelesaiannya adalah : {-2, -3}

Jawab : B

Soal No.7

Akar-akar dari persamaan kuadrat  x² − 6x + 9 = 0 adalah :

A. x1 = 3 dan x2 = 3
B. x1 = 3 dan x2 = -3
C. x1 = -3 dan x2 = -3
D. x1 = -3 dan x2 = 3

Pembahasan

Dalam pembahasan kali ini kita akan menggunakan Rumus ABC. Dari persamaan :  x² − 6x + 9 = 0, didapatkan  nilai a = 1, b = -6 dan c = 9
Sehingga akar pertamanya

x1 = 

−(−6) – √(−6)2 – 4(1)(9)2(1)

 

x1 = 

6 – √36 – 362

 

x1 = 

6 – 02

 

x1 = 

62

 

x1 = 3


Sedangkan untuk nilai akar keduanya adalah :

x2 = 

−(−6) + √(−6)2 – 4(1)(9)2(1)

 

x2 = 

6 + √36 – 362

 

x2 = 

6 + 02

 

x2 = 

62

 

x2 = 3

Dengan demikian , kita dapatkan x1 = 3 dan x2 = 3

Jawab : A

Soal No.8

Terdapat salah satu akar dari persamaan kuadrat x2 + 2x + c = 0 adalah 3, maka akar lainnya adalah ….

A. x = -5
B. x = 5
C. x = 3
D. x = 15

Pembahasan

Substitusi nilai x = 3 ke dalam persamaan :
⇔ x2 + 2x + c = 0
⇔ 32 + 2.3 + c = 0
⇔ 9 + 6 + c = 0
⇔ c = -15

Kemudian kita masukkan nilai c nya :
⇔ x2 + 2x + c = 0
⇔ x2 + 2x + -15 = 0

Tahap berikutnya kita faktorkan untuk mendapatkan akar-akarnya :
⇔ x2 + 2x – 15 = 0
⇔ (x + 5)(x – 3) = 0
⇔ x = -5 atau x = 3

Jawab : A

Soal No.9

Nilai determinan dari x2 + 7x + 12 = 0 adalah….

A. 1
B. 2
C. 3
D. 11

Pembahasan

Jika diberi persamaan kuadrat ax2 + bx + c = 0 , maka cara mencari diskriminannya adalah :

D = b2 - 4ac
Dimana :
D = Nilai Diskriminan 
b = koefisien dari x >
a = koefisien dari x2
c = konstanta


Dengan demikian kita dapat cari determinannya :

Dari persamaan  x2 + 7x + 12 = 0, didapatkan :
nilai a = 1
nilai b = 7
nilai c = 12
D = 72 - 4(1)(12)
D = 49 - 48
D = 1


Jawab : A

Soal No.10

Nilai determinan dari 2×2 – 5x – 3 = 0 adalah ….

A. 49
B. 29
C. 39
D. 19

Pembahasan

Dari persamaan 2x2 – 5x – 3 = 0, didapatkan :
nilai a = 2
nilai b = -5
nilai c = -3
D = 52 – 4(2)(-3)
D = 25 + 24
D = 49

Jawab : A

Soal No.11

Jika akar-akar persamaan x2 – 3x – 10 = 0 adalah x1 dan x2, maka hasil penjumlahan dari x1 + x2 adalah ….

A. x1 + x2 = 3
B. x1 + x2 = 5
C. x1 + x2 = -3
D. x1 + x2 = 13

Pembahasan

Dengan metode pemfaktoran
⇔ x2 – 3x – 10 = 0
⇔ (x + 2)(x – 5) = 0
⇔ x1 = -2 dan x2 = 5

Jumlah akar-akarnya adalah :
⇔ x1 + x2 = -2 + 5
⇔ x1 + x2 = 3

Dengan menggunakan rumus Untuk mencari penjumlah, pengurangan akar dan perkalian dari akar-akarnya, kita dapat menggunakan rumus :

1.Jumlah Akar : x1 + x2 = -ba
2.Perkalian Akar : x1 . x2= ca
3.Selisih Akar : |x1-x2|= √D|a|

Untuk penjelesan lebih lengkapnya, silahkan kunjungi artikel dengan judul : Latihan Soal Sifat-Sifat Persamaan Kuadrat Dan Pembahasannya

Dengan demikian, jumlah akar-akarnya dapat kita cari dengan rumus sbb :
x1 + x2 = –

ba

x1 + x2 = –

(-3)1

= 3

Jawab : A

Soal No.12

Jika diketahui suatu persamaan kuadrat: x2 + 5x – 6 = 0 yang memiliki akar x1 dan x2. Maka hasil dari penjumlah kedua akar tersebut (x1 + x2) adalah …

A. 5
B. -5
C. 7
D. 15

Pembahasan

Dari persamaan x2 + 5x – 6 = 0, kita dapatkan :
a = 1, b = 5 dan c = -6

x1 + x2 = –

ba

x1 + x2 = –

51

= -5

Jawab : B

Soal No.13

Suatu persamaan kuadrat 2x2 – 12x + 6 = 0 memiliki akar-akar p dan q. Maka nilai perkalian akar-akarnya (p . q) adalah …..

A. 3
B. 6
C. -3
D. -2

Pembahasan

Dari persamaan 2x2 – 12x + 6 = 0, kita dapatkan :
a = 2, b = -12 dan c = 6

x1 . x2 =

ca

maka :
p . q =

ca

p . q =

62

= 3

Jawab : A

Soal No.14

Jika persamaan ax2 – 4x + 10 = 0 mempunyai akar-akar x1 dan x2 dengan x1 . x2 = 5, maka x1 + x2 = …..

A. -8
B. -4
C. -2
D. 2

Pembahasan

Dari persamaan : ax2 – 4x + 10 = 0 , kita dapatkan a=a, b=-4 dan c=10. Yang belum diketahui cuma nilai a, untuk itu kita perlu cari nilai “a” nya.

⇔ x1 . x2 = 5
⇔

10a

= 5
⇔ 10 = 5a
⇔ a =

105

= 2

x1 + x2 = –

ba

x1 + x2 = –

(-4)2

= 2

Jawab : D

Soal No.15

Salah satu akar persamaan 2x² – x – 4 = 0 adalah p. Maka nilai 4p⁴ – 4p³ + 3p² – p = ……?

A. 8
B. 12
C. 16
D. 20

Pembahasan

⇔ 2x² – x – 4 = 0
⇔ 2p² – p = 4
⇔ 2p² – p = 4 (Hasil 1)

Dari soal diketahui : 4p⁴ – 4p³ + 3p² – p, dapat kita faktorkan menjadi :
⇔ 4p⁴ – 4p³ + 3p² – p
⇔ (2p² – p)² + (2p² – p)
⇔ (4)² + (4)
⇔ 20

Maka :4p⁴ – 4p³ + 3p² – p = 20

Jawab : D

Check Also

Contoh Soal Luas dan Keliling Jajaran Genjang Beserta Pembahasannya

Contoh Soal Luas dan Keliling Jajaran Genjang Beserta Pembahasannya

Contoh Soal Luas dan Keliling Jajaran Genjang – Pada artikel ini akan disajikan pembahasan soal-soal …

Teknobae.com
© Copyright 2024, All Rights Reserved